Интеллект-карты в геометрии
Интеллект-карты в геометрии ( в просторечии – шпаргалки)
Сайт доступен по новому адресу dnu-edu.ru.
Бирюкова С.С. Москва
Геометрию преподавать труднее, чем алгебру; я думаю, что с этим согласны все учителя математики. В алгебре накопленные знания легко выстраиваются в линеечку: линейные уравнения – линейные неравенства – квадратные уравнения – квадратные неравенства, и
так далее. Другие факты обвивают эту линейку, и получается вполне компактная структура. В геометрии же число теорем и определений, необходимых для решения задач, настолько велико, что они разрастаются в ветвистое дерево, на ветвях которого вместо листьев висят длинные тексты, связь между которыми давно утрачена. И эти тексты никак не хотят укладываться в голове у учащихся. А вот рисунки и символы запечатлеваются гораздо легче.
Лет семь назад я попыталась изобразить теоремы графически, то есть создать карту памяти, и каждой теореме, аксиоме, определению сопоставить картинку-ярлык. Моей задачей было создать геометрическое дерево, охватываемое взглядом.
Сначала учащиеся рисовали в тетради ярлыки доказанных теорем и пользовались шпаргалкой, чтобы вспомнить их при решении задач..
Работа напоминала примерку одежды: приложил одно платье – не подошло… другое… третье… ура! Оказалось впору.
Но успокаиваться было рано. Количество теорем росло, каждый раз рисовать их на доске становилось трудно.
Я стала делать шпаргалку в электронном виде в форме таблицы, отдельно заполняя строки с аксиомами, определениями и теоремами.
У такой шпаргалки был ряд существенных недостатков:
§ Уже к восьмому классу таблицу невозможно стало проецировать на экран целиком.
§ Дети рисовали свои шпаргалки на листах бумаги, которые постоянно теряли.
§ Теоремы было трудно группировать, приходилось переделывать всю таблицу.
Тогда я поняла, что для решения проблем более всего подходит составление ментальных карт или интеллект-карт. Аналог этого метода в 60-х годах прошлого века был известен как метод В. Ф. Шаталова. К сожалению, он нашёл небольшое число последователей. Ментальные карты позволяют графически отображать информацию, вносить динамику и разнообразие в записи при помощи цвета и выделения, указывать взаимосвязи между отдельными элементами. Информацию легко пополнять, рисунки быстро распознаются и усваиваются.
Следующим этапом стало использование программы «Живая геометрия», в которой и выполнялись рисунки, тем более что мы перешли к работе с задачами именно в этой программе. Уроки геометрии стали проходить в компьютерном классе.
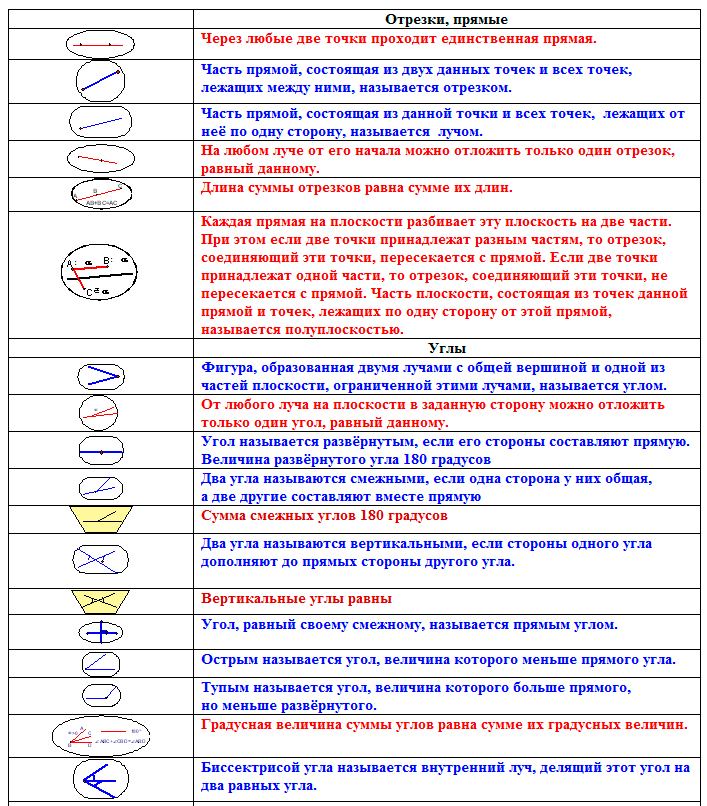
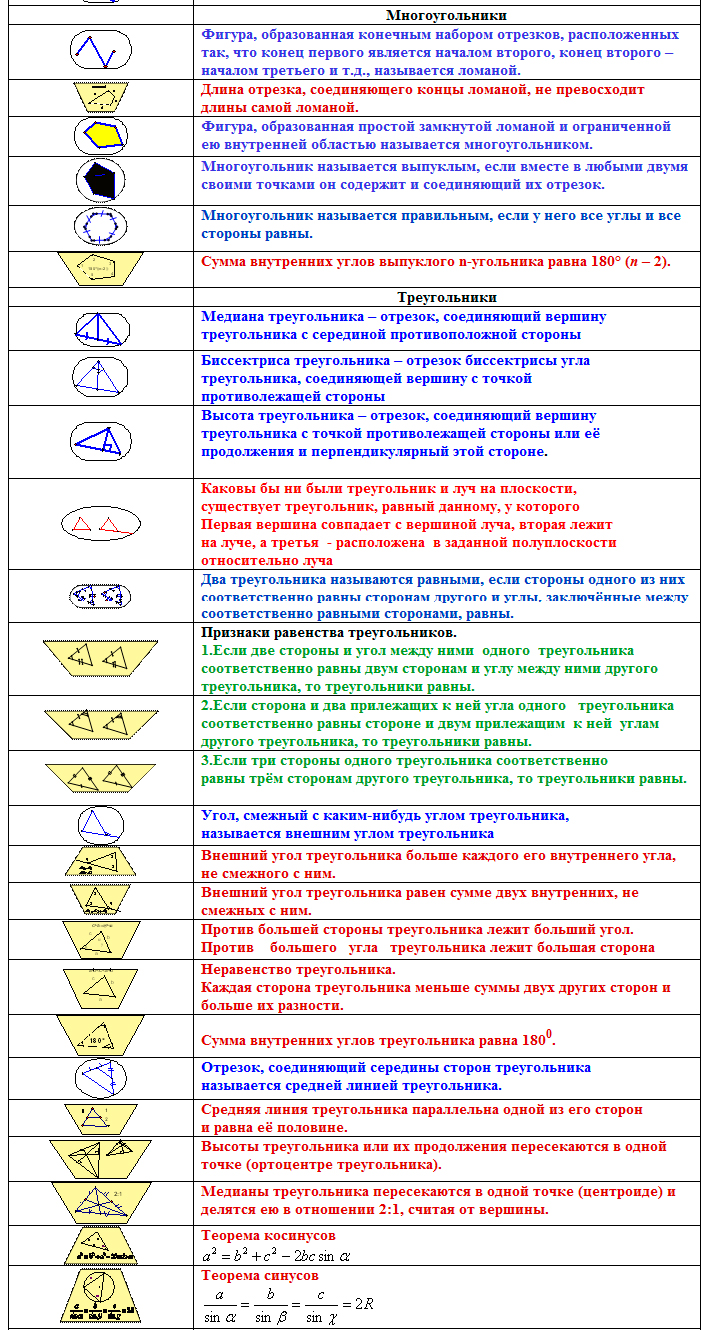
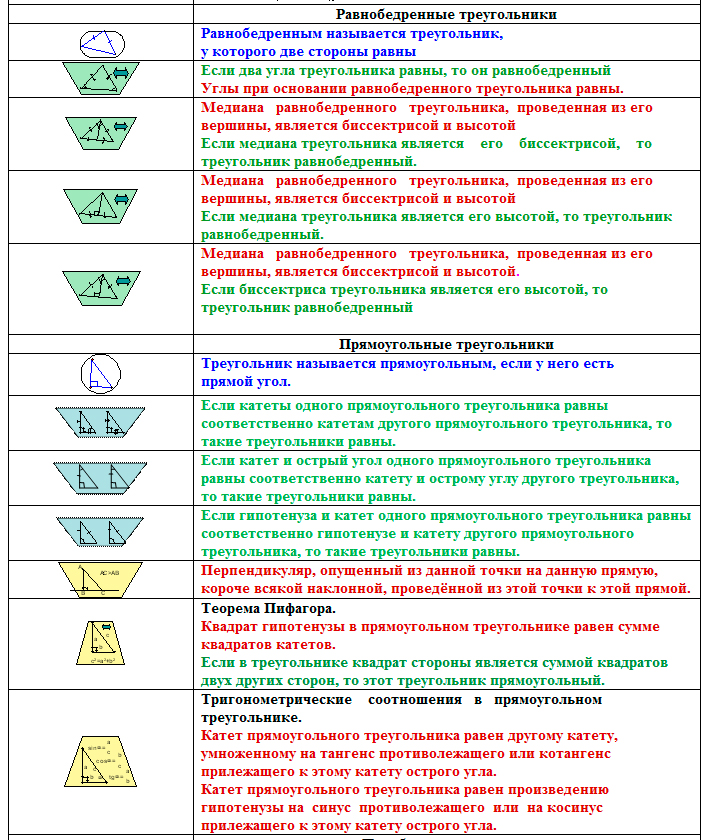
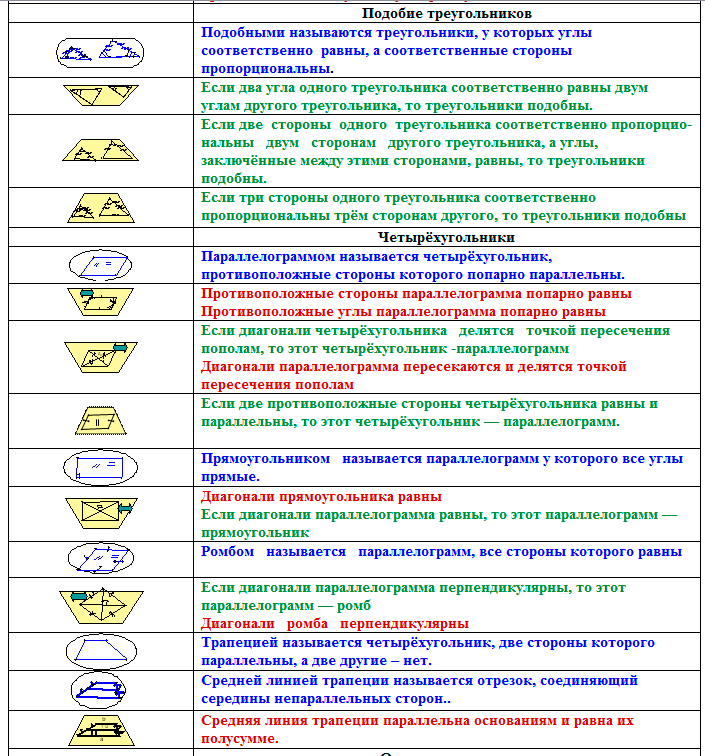
На рисунке представлена одна из таких карт памяти.
——————
Одно из её достоинств заключается в том, что каждый учитель легко может поправить или дополнить её под себя и своих учеников.
Кроме того, учащиеся дома на своих компьютерах могут структурировать её так, как им удобно.
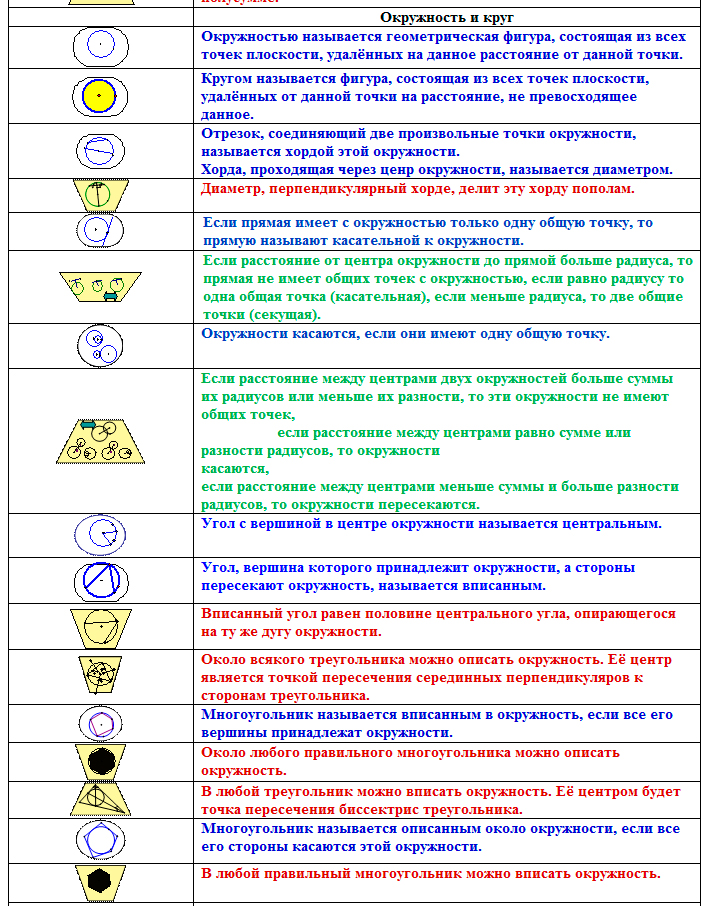
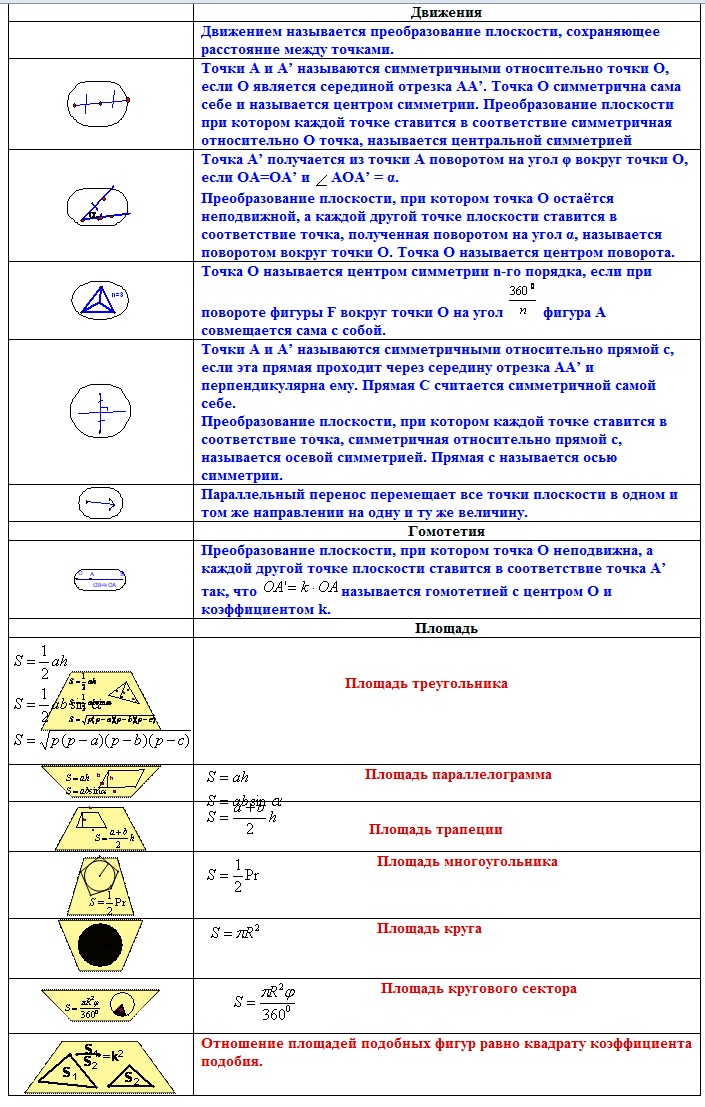
Но это не решило проблему запоминания текста теорем. Поэтому была создана шпаргалка с формулировками, фрагмент которой приведён ниже. Аксиомы выделялись в ней красным цветом, определения – синим, а теоремы – зелёным и бордовым цветами: бордовым — свойства, зелёным – признаки.